故障樹分析（Fault Tree Analysis, FTA）

    故障樹分析（FTA）技術是美國貝爾電話實驗室于1962年開發的，它采用邏輯的方法，形象地進行危險的分析工作，特點是直觀、明了，思路清晰，邏輯性強，可以做定性分析，也可以做定量分析。體現了以系統工程方法研究安全問題的系統性、準確性和預測性，它是安全系統工程的主要分析方法之一。一般來講，安全系統工程的發展也是以故障樹分析為主要標志的。

    1974年美國原子能委員會發表了關于核電站危險性評價報告，即“拉姆森報告”，大量、有效地應用了FTA，從而迅速推動了它的發展。

    1 數學基礎

    1.1基本概念

    (1)集：從最普遍的意義上說，集就是具有某種共同可識別特點的項（事件）的集合。這些共同特點使之能夠區別于他類事物。

    （2）并集

    把集合A的元素和集合B的元素合并在一起，這些元素的全體構成的集合叫做A與B的并集，記為A∪B或A＋B。

    若A與B有公共元素，則公共元素在并集中只出現一次。

    例 若A={a、b、c、d}；

     　　B={c、d、e、f}；

     　　 AUB= {a、b、c、d、e、f}。

    （3）交集

    兩個集合A與B的交集是兩個集合的公共元素所構成的集合，記為A∩B或A·B。

    根據定義，交是可以交換的，即A∩B=B∩A

    例若 A={a、b、c、d}；

     　　B={c、d、e}；

    則A∩B={c、d}。

    （4）補集

    在整個集合（Ω）中集合A的補集為一個不屬于A集的所有元素的集。補集又稱余，記為A′或A。

    1.2 布爾代數規則

    布爾代數用于集的運算，與普通代數運算法則不同。它可用于故障樹分析，布爾代數可以幫助我們將事件表達為另一些基本事件的組合。將系統失效表達為基本元件失效的組合。演算這些方程即可求出導致系統失效的元件失效組合（即最小割集），進而根據元件失效概率，計算出系統失效的概率。

    布爾代數規則如下（X、Y代表兩個集合）：

    （1）交換律 X·Y=Y·X

     　　X＋Y=Y＋X

    （2）結合律 X·（Y·Z）=（X·Y）·Z

     　　X＋（Y＋Z）=（X＋Y）＋Z

    （3）分配律 X·（Y＋Z）=X·Y＋X·Z

     　　X＋（Y·Z）=（X＋Y）·（X＋Z）

    （4）吸收律 X·（X＋Y）=X

     　　X＋（X·Y）=X

    （5）互補律 X＋X′=Ω=1

     　　X·X′=Ф（Ф表示空集）

    （6）冪等律 X·X=X

     　　X＋X=X

    （7）狄．摩根定律 （X·Y）′=X′＋Y′

     　　（X＋Y）′=X′·Y′

    （8）對合律 （X′）′= X

    （9）重疊律 X＋X′Y= X＋Y=Y＋Y′X

    2 故障樹的編制

    故障樹是由各種事件符號和邏輯門組成的，事件之間的邏輯關系用邏輯門表示。這些符號可分邏輯符號、事件符號等。

    2.1故障樹的符號及意義

    （1） 事件符號

    ①矩形符號：代表頂上事件或中間事件，見圖8－1（a）。是通過邏輯門作用的、由一個或多個原因而導致的故障事件。

    ②圓形符號：代表基本事件，見圖8－1（b）。表示不要求進一步展開的基本引發故障事件。

    ③屋形符號：代表正常事件，見圖8－1（c）。即系統在正常狀態下發揮正常功能的事件。

    ④菱形符號：代表省略事件，見圖8－1（d）。因該事件影響不大或因情報不足，因而沒有進一步展開的故障事件。

    ⑤橢圓形符號：代表條件事件，見圖8－1（e）。表示施加于任何邏輯門的條件或限制。

   

    (a) (b) (c) (d) (e)

    圖8－1 事件符號

    （2）邏輯符號

    故障樹中表示事件之間邏輯關系的符號稱門，主要有以下幾種。

    ①或門：代表一個或多個輸入事件發生，即發生輸出事件的情況。或門符號見圖8－2（a），或門示意圖見圖8－3。  

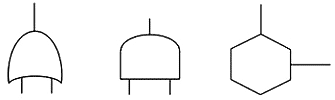
    圖8－2 邏輯符號

   

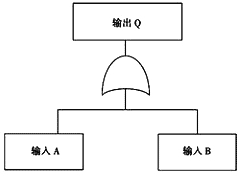
    圖8－3 或門示意圖

    ②與門：代表當全部輸入事件發生時，輸出事件才發生的邏輯關系。表現為邏輯積的關系。與門符號見圖8－2（b），與門示意圖見圖8－4。

   

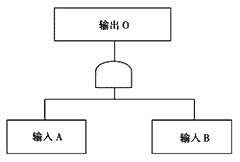
    圖8－4 與門示意圖

    ③禁門：是與門的特殊情況。它的輸出事件是由單輸入事件所引起的。但在輸入造成輸出之間，必須滿足某種特定的條件。禁門符號見圖8－2（c），禁門示意圖見圖8－5。

   

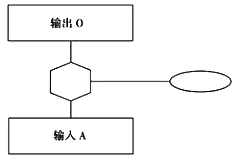
    圖8－5 禁門示意圖

    例如 許多化學反應只有在催化劑存在的情況下才能反應完全，催化劑不參加反應，但它的存在是必要的。這種邏輯如圖8－6所示。

   

    圖8－6 禁門舉例

    2.2建樹原則

    故障樹的樹形結構是進行分析的基礎。故障樹樹形結構正確與否，直接影響到故障樹的分析及其可靠程度。因此，為了成功地建造故障樹，要遵循一套基本規則。

    （1）“直接原因原理”（細步思考法則）

    編制故障樹時，首先從頂上事件分析，確定頂上事件的直接、必要和充分的原因，應注意不是頂上事件的基本原因。將這直接、必要和充分原因事件作為次頂上事件（即中間事件），再來確定它們的直接、必要和充分的原因，這樣逐步展開。這時，“直接原因”是至關重要的。按照直接原因原理，才能保持故障樹的嚴密的邏輯性，對事故的基本原因作詳盡的分析。

    （2）基本規則Ⅰ

    事件方框圖內填入故障內容，說明什么樣的故障，在什么條件下發生。

    （3）基本規則Ⅱ

    對方框內事件提問：“方框內的故障能否由一個元件失效構成？”

    如果對該問題的回答是肯定的，把事件列為“元件類”故障。如果回答是否定的，把事件列為“系統類”故障。

    “元件類”故障下，加上或門，找出主因故障、次因故障、指令故障或其他影響。

    “系統類”故障下，根據具體情況，加上或門、與門或禁門等，逐項分析下去。

    主因故障為元件在規定的工作條件范圍內發生的故障。如：設計壓力P0的壓力容器在工作壓力P≤P0時的破壞。

    次因故障為元件在超過規定的工作條件范圍內發生的故障。如：設計壓力為 ?P0的壓力容器在壓力P>P0時的破壞。

    指令故障為元件的工作是正常的，但時間發生錯誤或地點發生錯誤。

    其他影響的故障：主要指環境或安裝所致的故障，如濕度太大、接頭銹死等。

    （4）完整門規則

    在對某個門的全部輸入事件中的任一輸入事件作進一步分析之前，應先對該門的全部輸入事件作出完整的定義。

    （5）非門門規則

    門的輸入應當是恰當定義的故障事件，門與門之間不得直接相連，門門連接的出現說明粗心。在定量評定及簡化故障樹時，門門連接可能是對的，但在建樹過程中會導致混亂。

    2.3故障樹分析步驟

    （1）確定所分析的系統

    確定分析系統即確定系統所包括的內容及其邊界范圍。

    （2）熟悉所分析的系統

    指熟悉系統的整個情況，包括系統性能、運行情況、操作情況及各種重要參數等，必要時要畫出工藝流程圖及布置圖。

    （3）調查系統發生的事故

    調查分析過去、現在和未來可能發生的故障，同時調查本單位及外單位同類系統曾發生的所有事故。

    （4）確定故障樹的頂上事件

    是指確定所要分析的對象事件。將易于發生且后果嚴重的事故作為頂上事件。

    （5）調查與頂上事件有關的所有原因事件。

    （6）故障樹作圖

    按建樹原則，從頂上事件起，一層一層往下分析各自的直接原因事件，根據彼此間的邏輯關系，用邏輯門連接上下層事件，直到所要求的分析深度，形成一株倒置的邏輯樹形圖，即故障樹圖。

    （7）故障樹定性分析

    定性分析是故障樹分析的核心內容之一。其目的是分析該類事故的發生規律及特點，通過求取最小割集（或最小經集），找出控制事故的可行方案，并從故障樹結構上、發生概率上分析各基本事件的重要程度，以便按輕重緩急分別采取對策。

    （8）定量分析

    定量分析包括①確定各基本事件的故障率或失誤率；②求取頂上事件發生的概率，將計算結果與通過統計分析得出的事故發生概率進行比較。

    （9）安全性評價

    根據損失率的大小評價該類事故的危險性。這就要從定性和定量分析的結果中找出能夠降低頂上事件發生概率的最佳方案。

    2.4建樹舉例

    如圖8－7所示為一受壓容器裝置，配有安全閥及壓力自控裝置。壓力容器爆炸故障樹分析圖示于圖8－8。

   

    圖8－7 受壓容器裝置

   

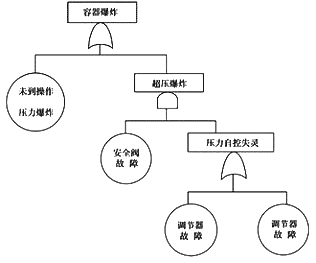
    圖8－8 壓力容器爆炸故障樹分析圖

    3 故障樹定性分析

    故障樹分析，包括定性分析和定量分析兩種方法。在定性分析中，主要包括最小割集、最小徑集和重要度分析。限于篇幅，以下僅介紹定性分析中的最小割集和最小徑集。

    3.1最小割集及其求法

    割集：它是導致頂上事件發生的基本事件的集合。最小割集就是引起頂上事件發生必須的最低限度的割集。最小割集的求取方法有行列式法、布爾代數法等。現在，已有計算機軟件求取最小割集和最小徑集。以下簡要介紹布爾代數化簡法。

    圖8－9為一故障樹圖，以下是用布爾代數化簡的過程。

   

    圖8－9 故障樹

    T=A1＋A2

     =X1 X2 A3＋X4 A4

     =X1 X2 (X1＋X3)＋ X4 (X5＋X6)

     =X1 X2 A1＋X1 X2 A3＋ X4 X5＋X4 X6

     =X1 X2＋ X4 X5＋X4 X6

    所以最小割集為{X1，X2}，{X4，X5}，{X4，X6}。結果得到三個交集的并集，這三個交集就是三個最小割集E1={X1，X2}，E2={X4，X5}，E3={X4，X6}。用最小割集表示故障樹的等效圖如圖8－10。

   

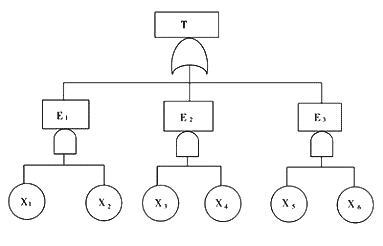
    圖8－10 故障樹等效樹（用最小割表示）

    3.2最小徑集及其求法

    徑集：如果故障樹中某些基本事件不發生，則頂上事件就不發生，這些基本事件的集合稱為徑集。

    最小徑集：就是頂上事件不發生所需的最低限度的徑集。

    最小徑集的求法是利用它與最小割集的對偶性。首先作出與故障樹對偶的成功樹，即把原來故障樹的與門換成或門，而或門換成與門，各類事件發生換成不發生，利用上述方法求出成功樹的最小割集，再轉化為故障樹的最小徑集。

    例： 將上例中故障樹變為成功樹

    用T'、 A'1、 A'2、 A'3、 A'4、 X'1、 X'2、 X'3、 X'4、X'5、 X'6表示事件T、 A1、 A2 、A3、 A4、 X1、 X2、 X3、 X'4、X5、 X6的補事件,即成功事件；邏輯門作相應轉換，如圖8－11。

   

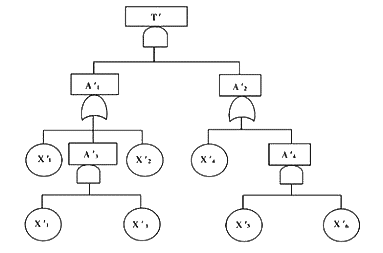
    用布爾代數化簡法求成功樹的最小割集：

    T'= A'1 ·A'2

    　=(X'1＋A'3＋X'2)·(X'4＋A'4)

    　=(X'1＋X'2＋X'1 X'3)·(X'4＋ X'5 X'6)

    　=(X'1＋X'2)·(X'4＋ X'5 X '6)

    　=X'1 X'4＋ X'1 X'5 X'6＋X'2 X'4＋ X'2 X'5 X'6

    成功樹的最小割集：{X'1，X'4}{X'1，X'5，X'6}{X'2，X'4}{X'2，X'5，X'6}。

    即故障樹的最小徑集：

    P1={X1，X4}　 P2={X1，X5，X6}

    P3={X2，X4} 　 　P4={X2,X5，X6}

    如將成功樹布爾化簡的最后結果變換為故障樹結構，則表達式為

    T=(X1＋X4)( X1＋X5＋X6)( X2＋X4)(X2 ＋ X5＋X6)形成了四個并集的交集，如　　用最小徑集表示故障樹則如圖8－12所示。

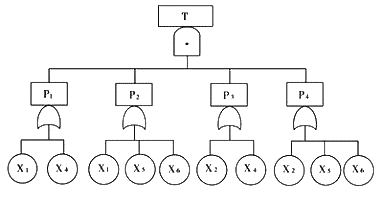
    圖8－12 故障樹的等效樹（用最小徑集表示）

    3.3最小割集和最小徑集在故障樹分析中的應用

    （1）最小割集表示系統的危險性

    求出最小割集可以掌握事故發生的各種可能，了解系統的危險性。

    每個最小割集都是頂上事件發生的一種可能，有幾個最小割集，頂上事件的發生就有幾種可能，最小割集越多，系統越危險。

    從最小割集能直觀地、概略地看出，哪些事件發生最危險，哪些稍次，哪些可以忽略，以及如何采取措施，使事故發生概率下降。

    例：共有三個最小割集{X1} 、{X2，X3} 、{X4，X5，X6，X7 ，X8}，如果各基本事件的發生概率都近似相等的話，一般地說，一個事件的割集比兩個事件的割集容易發生，五事件割集發生的概率更小，完全可以忽略。

    因此，為了提高系統的安全性，可采取技術、管理措施以便使少事件割集增加基本事件。

    就以上述三個最小割集的故障樹為例。可以給一事件割集{X1}增加一個基本事件X9，例如：安裝防護裝置或采取隔離措施等，使新的割集為{X1、X9}。這樣就能使整個系統的安全性提高若干倍，甚至幾百倍。若不從少事件割集入手，采取的措施收效不大。

    假設上述例中各事件概率都等于0.01，即q1= q2=q3=q4=q5=q6=q7=q8=q9=0.01。

    在未增加X9以前頂上事件發生的概率約為0.0101，而增加X9后概率近似為0.0002，使系統安全性提高了50倍，在可靠性設計中常用的冗長技術就是這個道理。注意，以上是各事件概率相等時采取的措施。采取防災措施必須考慮概率因素，若X1的發生概率極小，就不必考慮{X1}了。

    （2）最小徑集表示系統的安全性

    求出最小徑集可以了解到，要使頂上事件不發生有幾種可能的方案，從而為控制事故提供依據。

    一個最小徑集中的基本事件都不發生，就可使頂上事件不發生。故障樹中最小徑集越多，系統就越安全。

    從用最小徑集表示的故障樹等效圖可以看出，只要控制一個最小徑集不發生，頂上事件就不發生，所以可以選擇控制事故的最佳方案，一般地說，對少事件最小徑集加以控制較為有利。

    （3）利用最小割集、最小徑集進行結構重要度分析。

    （4）利用最小割集、最小徑集進行定量分析和計算頂上事件的概率等。